Antwort Wann brauche ich Cosinus? Weitere Antworten – Wann benutzt man den Cosinus

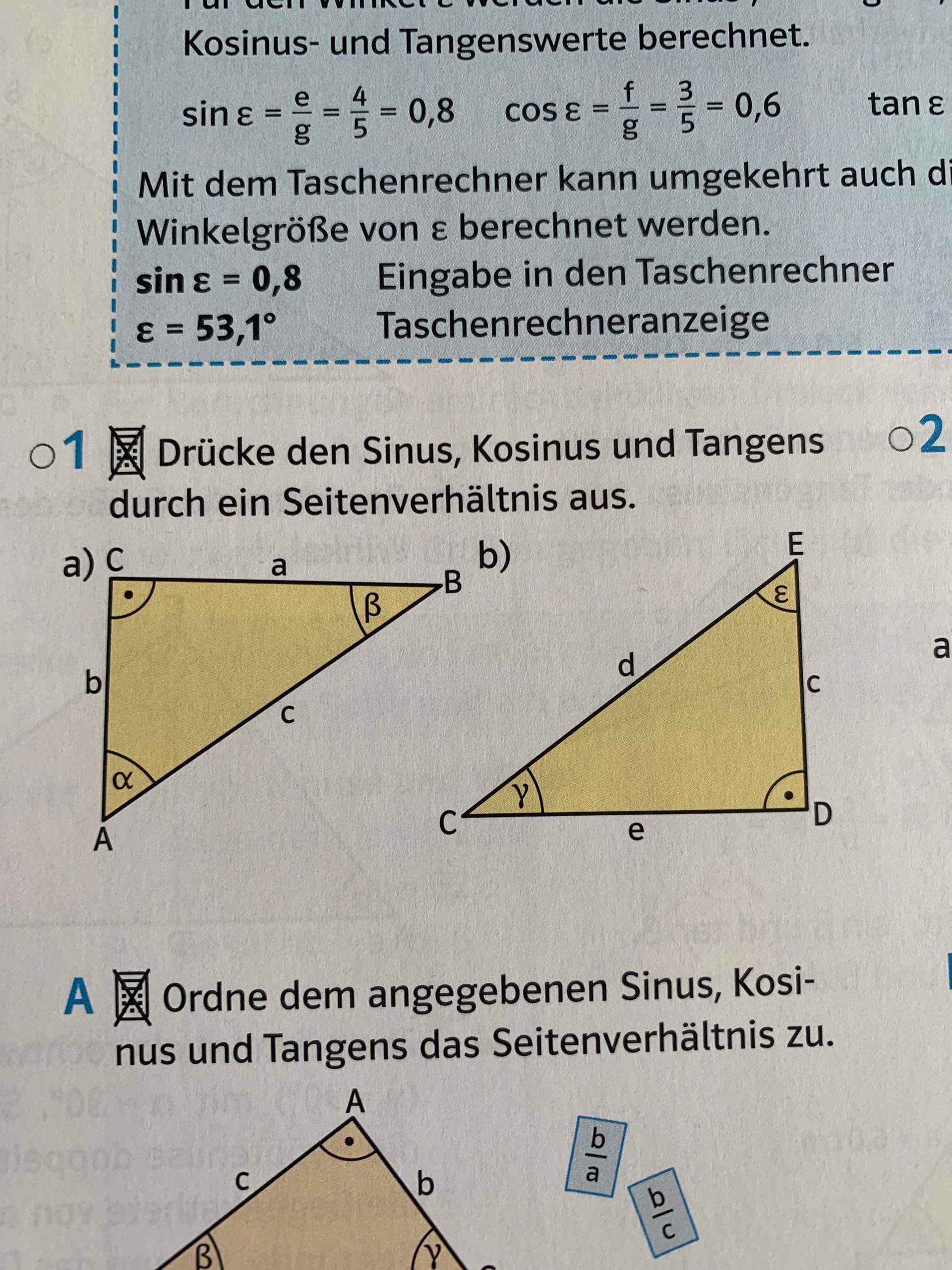
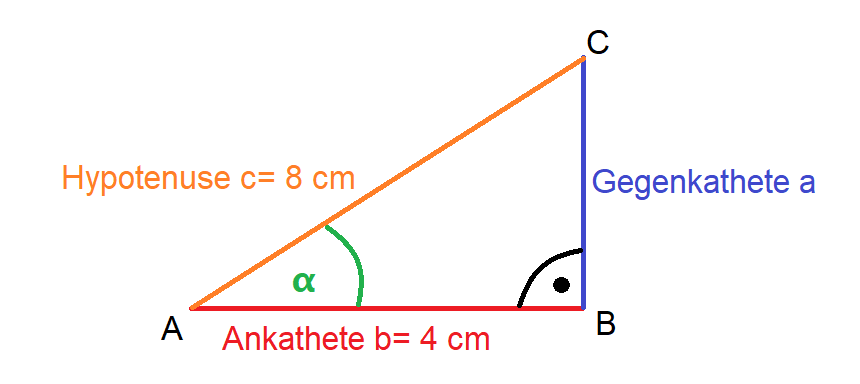
Mit dem Cosinus kannst du fehlende Winkel oder Seiten in einem rechtwinkligen Dreieck bestimmen. Dabei ist der Cosinus das Verhältnis zweier Seiten: der Ankathete und Hypotenuse des Dreiecks.Der Sinus eines Winkels ist das Verhältnis der Länge der Gegenkathete (Kathete, die dem Winkel gegenüberliegt) zur Länge der Hypotenuse (Seite gegenüber dem rechten Winkel). Der Kosinus ist das Verhältnis der Länge der Ankathete (das ist jene Kathete, die einen Schenkel des Winkels bildet) zur Länge der Hypotenuse.Der Sinus, der Cosinus und der Tangens werden angewendet, um Winkel und Seiten rechtwinkliger Dreiecke zu bestimmen.

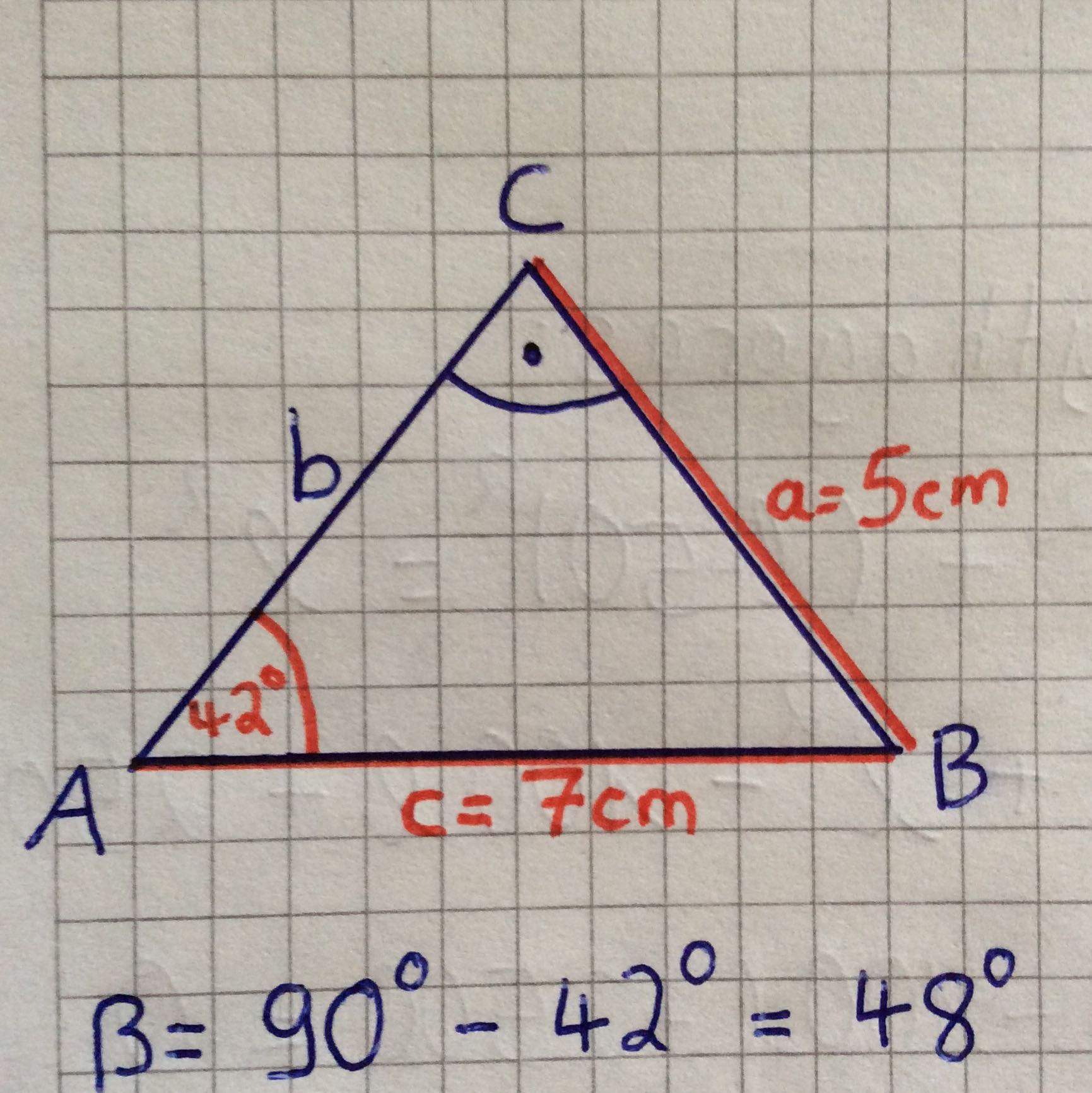
Wann kann ich den Kosinussatz anwenden : Den Kosinussatz kannst Du in einem beliebigen Dreieck anwenden, wenn Du eine Seite berechnen möchtest und die zwei anderen Seiten, sowie der davon eingeschlossene Winkel gegeben sind. Außerdem kannst Du ihn anwenden, wenn in einem Dreieck alle Seiten gegeben sind und Du einen Winkel berechnen möchtest.

Für was braucht man den Sinus

Mit dem Sinus kann man entweder die Länge der Hypotenuse oder die Länge der Gegenkathete oder die Größe des Winkels berechnen, je nachdem, welche der drei Größen gesucht ist. Die jeweils anderen beiden Größen müssen gegeben sein.

In welcher Klasse lernt man Cosinus : In Jahrgangsstufe 10 erweitern die Schüler die Definition von Sinus und Kosinus auf beliebige Winkel; dabei werden neben geometrischen ausdrücklich auch funktionale Aspekte der Trigonometrie vom Lehrplan eingefordert.

Sinussatz. Den Sinussatz kannst du benutzen, um fehlende Stücke eines Dreiecks zu berechnen. Zum Beispiel, wenn zwei Seitenlängen und ein gegenüber liegender Winkel oder eine Seitenlänge und zwei Winkel gegeben sind. Das Dreieck muss dabei nicht rechtwinklig sein!

Die Winkelfunktionen Sinus, Kosinus und Tangens verwendest du, wenn du die Länge einer Seite oder die Größe eines Winkels in einem rechtwinkligen Dreieck berechnen möchtest.

Wann brauche ich den Tangens

Mit dem Tangens rechnest du, wenn du zwei der drei Größen, Winkel, Ankathete des Winkels und Gegenkathete des Winkels gegeben hast und die dritte Größe suchst. Das Vorgehen ist also ähnlich wie beim Sinus und Kosinus.Der Kosinussatz gibt dir die Beziehung zwischen den drei Seiten und einem Winkel in einem Dreieck an. Er hilft dir dabei, aus zwei Seiten und dem eingeschlossenen Winkel die dritte Seite zu berechnen. aus drei Seiten einen Winkel zu berechnen.Der Satz des Pythagoras als Spezialfall des Kosinussatzes

Für γ = 9 0 ∘ \gamma=90^\circ γ=90∘ erhält man ein rechtwinkliges Dreieck und es gilt ⁡ ( 9 0 ∘ ) = 0 \cos(90^\circ)=0 cos(90∘)=0. Damit ist der Satz des Pythagoras c 2 = a 2 + b 2 c^2=a^2+b^2 c2=a2+b2 ein Spezialfall des Kosinussatzes.

Der Vorteil des Kosinussatzes ist, dass die Werte immer eindeutig sind. Man erhält für die Winkelberechnung einen Wert von 0° bis 180° . Beim Sinussatz hingegen erhält man stets einen Winkel von 0° bis 90° und muss das Ergebnis rechnerisch bzw. mit der gegebenen Zeichnung überprüfen.

Wo kann man Sinus anwenden : Mit dem Sinussatz kannst du Seiten und Winkel in jedem beliebigen Dreieck berechnen. Wenn du eine Seite und den gegenüberliegenden Winkel kennst, kannst du von einer anderen Größe (Seite oder Winkel) die gegenüberliegende Größe ausrechnen.

In welcher Klasse macht man Sinus und Cosinus : In Jahrgangsstufe 10 erweitern die Schüler die Definition von Sinus und Kosinus auf beliebige Winkel; dabei werden neben geometrischen ausdrücklich auch funktionale Aspekte der Trigonometrie vom Lehrplan eingefordert.

Für was braucht man den Sinussatz

Mit dem Sinussatz berechnest Du fehlende Seitenlängen oder Winkel in einem beliebigen Dreieck, solange Du nur „Seiten-Winkel-Paar“ und eine weitere Größe kennst.

Mit dem Kosinus kannst du rechnen, wenn du zwei der drei Größen, Winkel, Ankathete und Hypotenuse gegeben hast und die dritte suchst. Das Vorgehen ist also ähnlich wie beim Sinus, nur mit der Ankathete anstatt der Gegenkathete eines Winkels.Der Tangens wird mathematisch \tan(\alpha) abgekürzt. Neben dem Sinus und dem Kosinus gibt es auch noch den Tangens. Mit dem Tangens rechnest du, wenn du zwei der drei Größen, Winkel, Ankathete des Winkels und Gegenkathete des Winkels gegeben hast und die dritte Größe suchst.

Was ist die Cosinus Formel : sin(α)= Gegenkathete / Hypotenuse. cos(α)= Ankathete / Hypotenuse. tan(α)= Gegenkathete / Ankathete.