Antwort Was bringt mir die Varianz? Weitere Antworten – Ist eine hohe Varianz gut

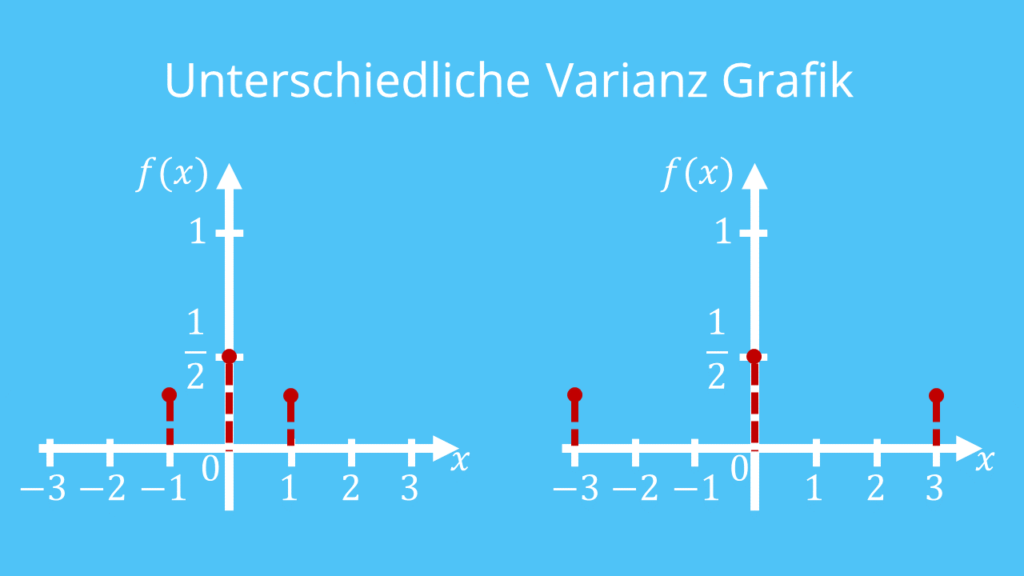
Ist die Varianz groß, so streuen die Werte eher stark um den Erwartungswert. Ist die Varianz gering, so streuen die Werte eher wenig um den Erwartungswert.Der Unterschied zwischen dem Streuungsparameter Varianz und der Standardabweichung ist also, dass die Standardabweichung die durchschnittliche Entfernung vom Mittelwert misst und die Varianz die quadrierte durchschnittliche Entfernung vom Mittelwert.Die Varianz ist ein Maß für die Abweichung einer Zufallsvariablen X von ihrem Erwartungswert μ in der Stochastik. Sie beschreibt die mittlere quadratische Abweichung der Werte der Zufallsvariablen zum Erwartungswert. Die Varianz einer Zufallsgröße ist eng mit ihrer Standardabweichung verknüpft.

Was sagt die Varianzaufklärung aus : Gibt an, welcher Anteil der Streuung (vgl. Varianz) eines abhängigen Merkmals auf die Veränderung von unabhängigen Merkmalen zurückzuführen ist.

Wie interpretiert man die Varianz

Varianz ist der statistische Ausdruck für die Streuung der Daten. Die Varianz gibt also an wie weit sich die Daten im Schnitt vom Mittelwert unterscheiden. Um so größer die Varianz umso weiter liegen die Daten vom Mittelwert entfernt.

Kann die Varianz größer 1 sein : Der Variationskoeffizient ist eine Normierung der Varianz : Ist die Standardabweichung größer als der Mittelwert bzw. der Erwartungswert , so ist der Variationskoeffizient größer 1.

Die Varianz gibt an, wie sich deine Beobachtungswerte um den Mittelwert aller Beobachtungen verteilen. Da sie die Streuung der Werte um den Mittelwert beschreibt, gehört die Varianz zu den Streuungsmaßen.

Das R² ist ein Gütemaß der linearen Regression. Es gibt an, wie gut die unabhängigen Variablen dazu geeignet sind, die Varianz der abhängigen zu erklären. Das R² liegt immer zwischen 0% (unbrauchbares Modell) und 100% (perfekte Modellanpassung).

Was geben Varianz und Standardabweichung an

Der Begriff der Streuungsmaße ist in der deskriptiven Statistik zu finden und fasst eine Vielzahl von Begriffen zusammen. Streuungsmaße geben die Ausbreitung und Streuung der Beobachtungswerte an. Die wichtigsten Vertreter sind die Varianz, die Standardabweichung und die Spannweite.Der Vorteil der Standardabweichung gegenüber der Varianz ist, dass die Standardabweichung die gleiche Masseinheit wie die ursprüngliche Variable hat.Die Varianz einer Zufallsvariable ist immer ≥ 0. Für eine konstante Zufallsvariable X = c gilt VarX = 0.

Die Zufallsvariablen sind nicht begrenzt auf reelle Werte, und die Anzahl der Werte zur Berechnung der Varianz kann auch unendlich sein. In der mathematischen Statistik ist die Varianz die erwartete quadratische Abweichung von Zufallsvariablen von ihrem Erwartungswert.