Antwort Was ist die Polynomfunktion 2 Grades? Weitere Antworten – Was ist eine Polynomfunktion zweiten Grades

Eine Polynomfunktion zweiten Grades der Variable x ist die Summe von 3 algebraischen Elementen, von denen eines eine Potenz zweiter Ordnung von x enthält. Die allgemeine Schreibweise (Normalform) lautet: a.x2 + b.x + c, a, b und c sind die Parameter der Funktion. c ist der y-Wert am Ursprung von f(x) : f(0) = c.Definition einer Polynomfunktion: Polynomfunktionen sind Funktionen, bei denen Potenzterme mit beliebigen natürlichen Exponenten, ggf. multipliziert mit einem Koeffizienten, addiert werden. heißen Koeffizienten des Polynoms.Um eine Funktion 2. Grades, also eine quadratische Funktion zu bestimmen, benötigen wir drei Punkte, die nicht sämtlich auf einer Geraden liegen dürfen. Dies liegt daran, dass drei Variablen bestimmt werden müssen. f(x) = ax^2+bx+c \rightarrow Die Variablen a, b und c müssen bestimmt werden.

Was versteht man unter dem Grad einer Polynomfunktion : höchster Exponent eines Polynoms. Für ein Polynom p(x) = anxn + an−1xn−1 +···+ a1x + a0 mit an ≠= 0 in einer Variablen nennt man den höchsten Exponenten n den Grad des Polynoms und schreibt n = grad(p) oder auch n = deg(p). Dabei steht deg für degree.

Wie viele Nullstellen hat eine Polynomfunktion 2 Grades

Ein Polynom vom Grad 2 kann also entweder keine, genau eine oder zwei Nullstellen in den reellen Zahlen haben. x1 = − 1 2 + 5 2 = 2, x2 = − 1 2 − 5 2 = −3.

Für was braucht man Polynomfunktion : Wofür werden Polynomfunktionen genutzt Die Polynomfunktionen können uns dabei helfen, den Verlauf von Straßen, Flüssen oder auch Baukonstruktionen aus der Architektur zu modellieren. In der Mathematik sind sie außerdem wichtig, weil man sehr viele komplizierte Funktionen mit Polynomfunktionen nähern kann.

Die höchste Potenz der Variablen x innerhalb des Funktionsterms gibt den Grad der Polynomfunktion an. Wenn also die höchste Potenz des Funktionsterms x3 ist, dann handelt es sich um eine Funktion dritten Grades. Genauso hat eine Polynomfunktion sechsten Grades als höchste Potenz einen Term mit x6.

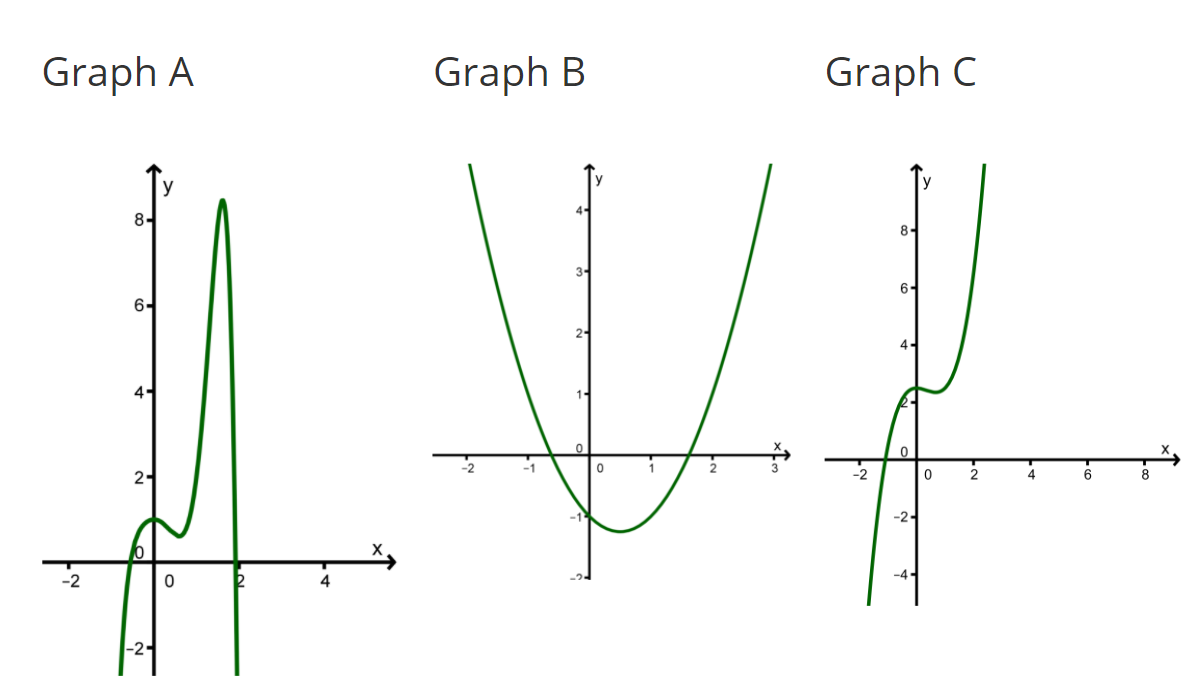
Aussehen von Polynomfunktionen

Gezeichnet sehen Polynome manchmal ganz komisch aus, wie hier. Der grüne Graph zeigt die Polynomfunktion f(x)=x3+3×2+1 das Orangenfarbende die Polynomfunktion f(x)=x5+4×3+2x+4. Polynome können mehrere Nullstellen, Hoch- und Tiefpunkte haben.

Wie viele Nullstellen hat eine Funktion 2 Grades

Deine beiden Nullstellen der quadratischen Funktion sind also x1 = -2 und x2 = 2. An einer Nullstelle ist der Wert einer quadratischen Funktion gleich 0, also f(x) = 0. Eine quadratische Funktion hat keine, eine oder zwei Nullstellen. Sie sind die Lösungen der quadratischen Gleichung ax2 + bx + c = 0.Grad einer Polynomfunktion erkennen

Der Grad einer Polynomfunktion wird durch ihren höchsten Exponenten bestimmt, wobei die Exponenten nicht in geordneter Reihenfolge stehen müssen. Die Polynomfunktion: f(x) ist ein Polynom dritten Grades, da der größte Exponent 3 ist.Wann hat eine quadratische Funktion zwei Nullstellen, eine Nullstelle oder keine Nullstelle Eine Funktion hat zwei Nullstellen, wenn die beiden Schenkel der Parabel die x-Achse schneiden. Sie hat nur eine Nullstelle, wenn nur der Scheitelpunkt der Parabel die x-Achse berührt.

Polynome sind Summe von Termen der Form k⋅xⁿ, wobei k eine beliebige Zahl und n eine positive ganze Zahl ist. Zum Beispiel ist 3x+2x-5 ein Polynom.

Wie berechnet man die Nullstellen einer Polynomfunktion : Die Nullstellen eines Polynoms berechnest Du, indem Du das ganze Polynom gleich 0 setzt. Wenn Du die Nullstellen eines Polynoms zweiten Grades berechnen sollst, nimmst Du die Mitternachtsformel. Bei Polynomfunktionen größeren Grades kannst Du entweder substituieren oder die Polynomdivision durchführen.

Wann ist es keine Polynomfunktion : Keine Polynome sind alle komplizierteren Terme, die beispielsweise Wurzeln oder Brüche enthalten, deren Nenner aus einer Variable besteht (gebrochen rationale Funktionen ).

Was sind einfache und doppelte Nullstellen

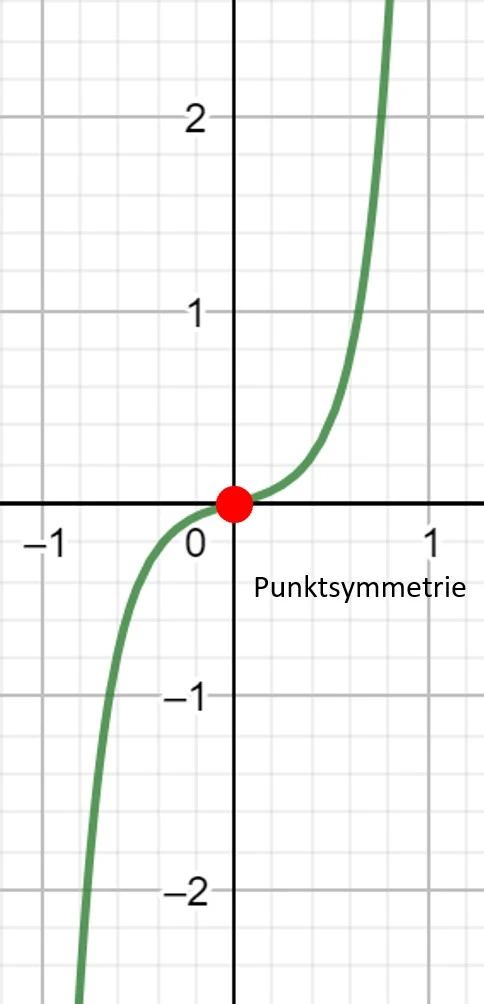
Allgemein gilt: Eine einfache Nullstelle sieht aus wie y = x, d.h. der Graph schneidet die x-Achse. Eine zweifache Nullstelle sieht aus wie y = x2, d.h. der Graph berührt die x-Achse. Eine dreifache Nullstelle sieht aus wie y = x3, d.h. der Graph schneidet die x-Achse.

Ein Polynom ist ein Term, der aus Summanden und/oder Subtrahenden bestehen kann. Diese sind innerhalb des Terms an dieselbe Variable mit verschiedenen Exponenten gebunden. Die allgemeine Formel für Polynome ist f ( x ) = a x n + b x n – 1 + c x n – 2 + d , wobei Polynome unendlich lang sein können.Das Aussehen von mehrfachen Nullstellen

Allgemein gilt: Eine einfache Nullstelle sieht aus wie y = x, d.h. der Graph schneidet die x-Achse. Eine zweifache Nullstelle sieht aus wie y = x2, d.h. der Graph berührt die x-Achse. Eine dreifache Nullstelle sieht aus wie y = x3, d.h. der Graph schneidet die x-Achse.