Antwort Was sind Polstellen und asymptoten? Weitere Antworten – Was ist eine Polstelle einfach erklärt

Eine Polstelle (auch: ein Pol, eine Unendlichkeitsstelle) ist ein x-Wert, bei dem der Graph einer Funktion eine senkrechte (vertikale) Asymptote hat, also der Funktionswert gegen±∞ divergiert. An dieser Stelle ist die Funktion daher nicht definiert, weswegen man auch von einer Definitionslücke spricht.Eine Asymptote ist eine Kurve oder Linie (Gerade), an die sich der Graph einer Funktion immer weiter annähert. Im Unendlichen wird der Abstand zwischen dem Graphen und der Asymptote somit sehr klein. Um Asymptoten zu berechnen, musst du verschiedene Arten unterscheiden: senkrechte Asymptote bei Nenner = 0.Polstellen berechnen

1. Schritt 1: Nullstellen des Nenners berechnen; hier werden die Definitionslücken bestimmt.
2. Schritt 2: Nullstellen des Zählers berechnen.
3. Schritt 3: Falls Zähler und Nenner gemeinsame Nullstellen haben, die Vielfachheit der gemeinsamen Nullstellen für Zähler (die Zahl ) und Nenner (die Zahl.

Wie berechne ich die Asymptoten : Wenn der Zählergrad kleiner ist als der Nennergrad. In diesem Fall ist die x-Achse die waagerechte Asymptote. Wenn der Zählergrad gleich dem Nennergrad ist. Dann lässt sich die waagerechte Asymptote berechnen, indem man die Faktoren vor der höchsten Potenz im Zähler durch den Faktor der höchsten Potenz im Nenner teilt.

Wann liegt keine Polstelle vor

Wird der Nenner ungleich null, so liegt eine hebbare Definitionslücke vor. Wird der Nenner hingegen null, so liegt eine Polstelle vor.

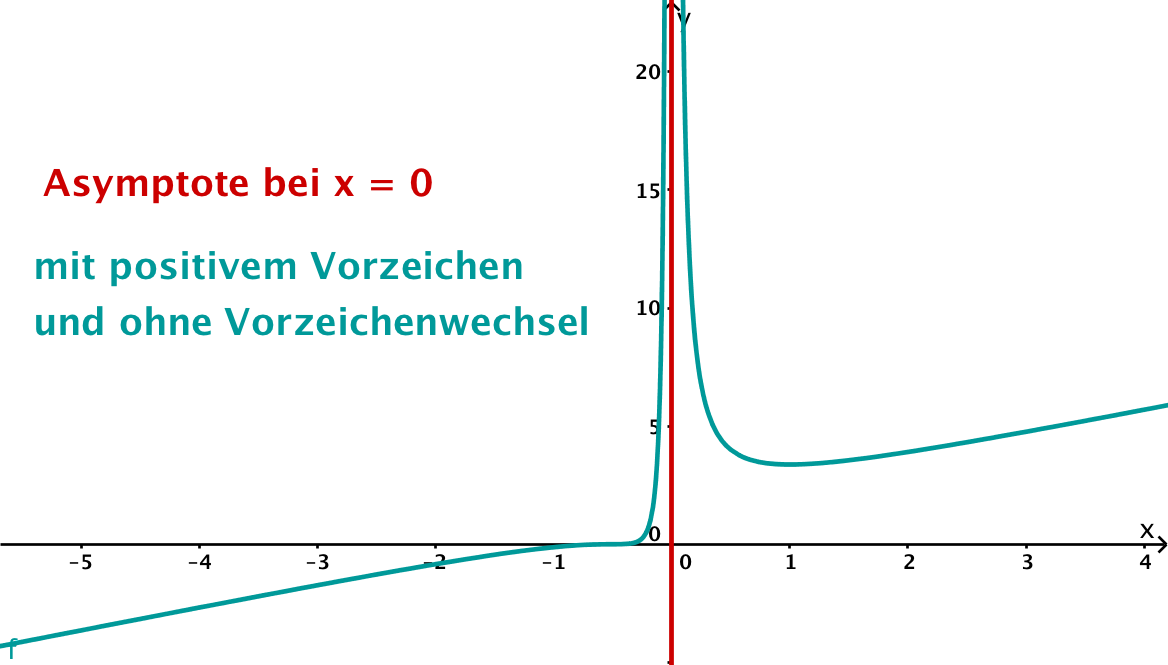
Wann hat eine Funktion keine Polstelle : Die Funktion besitzt an der Stelle x 0 = 0 eine Polstelle. Die y-Achse ist in diesem Fall die sogenannte Polgerade.

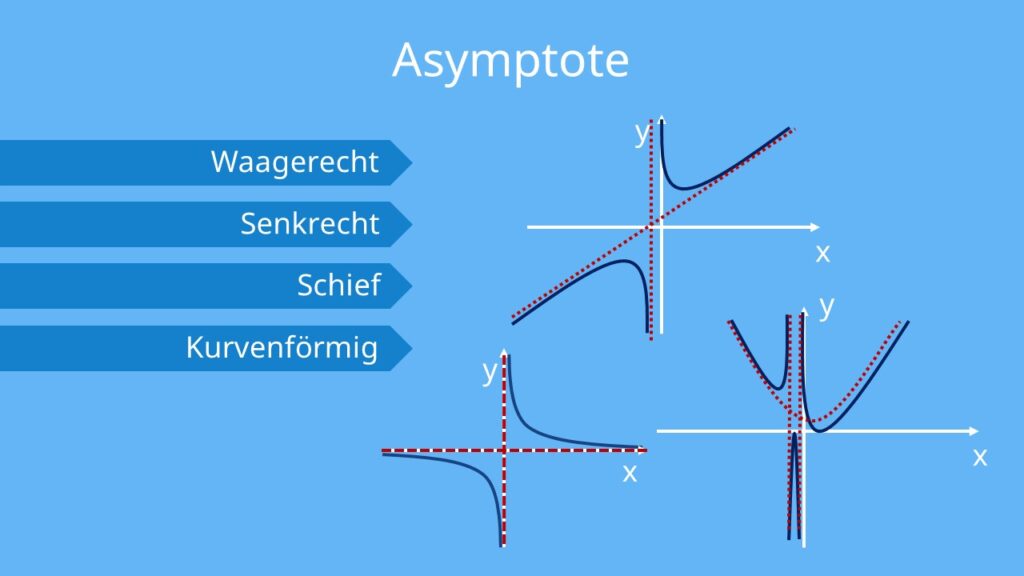
Man unterscheidet drei verschiedene Arten von Asymptoten: senkrechte Asymptote. waagerechte Asymptote. schiefe Asymptote.

Eine waagerechte Asymptote liegt immer dann vor, wenn der Zählergrad kleiner oder gleich dem Nennergrad ist.

Ist jede Definitionslücke eine Polstelle

Es gibt zwei Arten von Definitionslücken: Polstellen und hebbare Definitionslücken. ist zusätzlich zum Nenner auch der Zähler 0 und die Lücke wird zum „Loch“. ist der Zähler ungleich 0.Sie sind spezielle Geraden oder Kurven, denen sich der Graph einer Funktion unendlich nah annähert und die in manchen Fällen auch von diesem geschnitten werden. Man kann auch sagen, die Funktion schmiegt sich an ihre Asymptote an, wenn der x- oder y-Wert der Funktion immer weiter Richtung +∞ oder -∞ verläuft.Das asymptotische Verhalten der e-Funktion ergibt sich aus der Tatsache, dass =0 ist und die e-Funktion damit den Grenzwert 0 hat, bzw. die x-Achse mit y=0 die Asymptote ist. Um den Grenzwert von Funktionen zu berechnet, wird für x entweder + unendlich oder – unendlich eingesetzt.

Eine gebrochenrationale Funktion mit einem Nennerpolynom vom Grad besitzt höchstens Definitionslücken. Eine Definitionslücke (Nullstelle des Nennerpolynoms), die nicht zugleich Nullstelle des Zählerpolynoms ist heißt Polstelle.

Wie viele Asymptoten gibt es : Man unterscheidet drei verschiedene Arten von Asymptoten: senkrechte Asymptote. waagerechte Asymptote. schiefe Asymptote.

Wann Polstelle und Lücke : Wird der Nenner ungleich null, so liegt eine hebbare Definitionslücke vor. Wird der Nenner hingegen null, so liegt eine Polstelle vor.

Sind asymptoten Definitionslücken

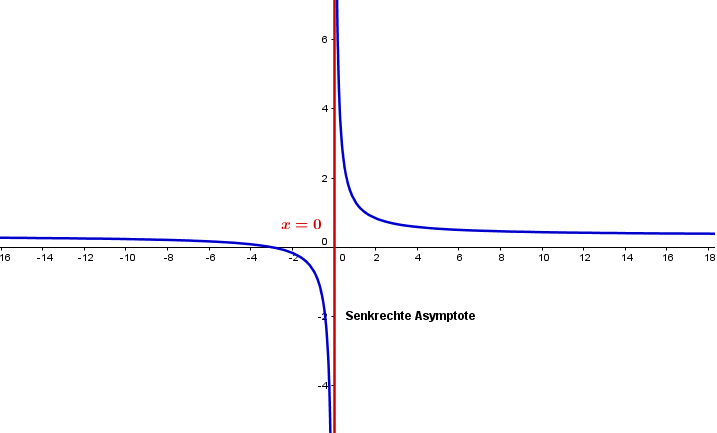
Senkrechte Asymptote

Die Funktion ist nicht für alle Zahlen definiert. Sie besitzt dort Definitionslücken, für die der Nenner Null wird. Diese Definitionslücken befinden sich bei x=-3 und x=3.

Polstellen, Definitionslücken

Eine gebrochenrationale Funktion mit einem Nennerpolynom vom Grad besitzt höchstens Definitionslücken. Eine Definitionslücke (Nullstelle des Nennerpolynoms), die nicht zugleich Nullstelle des Zählerpolynoms ist heißt Polstelle.Eine waagerechte Asymptote liegt immer dann vor, wenn der Zählergrad kleiner oder gleich dem Nennergrad ist.

Was ist der Unterschied zwischen Polstelle und Definitionslücke : Definitionslücken sind die Nullstellen des Nennerpolynoms q(x) einer gebrochen rationalen Funktion f : x ↦ p ( x ) q ( x ) . Eine Nullstelle des Nennerpolynoms ist eine Polstelle, wenn sie keine Nullstelle des Zählerpolynoms ist oder die Vielfachheit der Nullstelle im Nennerpolynom größer als im Zählerpolynom ist.