Antwort Welche Winkelfunktion gibt es? Weitere Antworten – Wie viele Winkelfunktionen gibt es
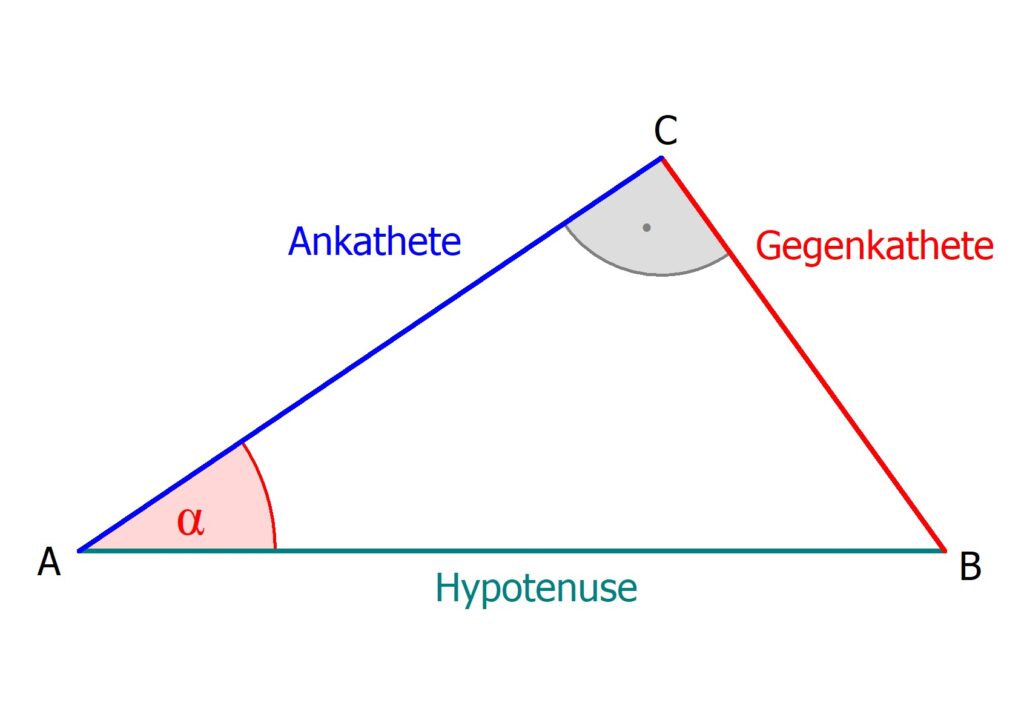
Für Berechnungen an rechtwinkligen Dreiecken sind die Winkelfunktionen wichtig. Man unterscheidet drei Winkelfunktionen: Sinus, Kosinus und Tangens.Dann sind die Formeln für die Winkelfunktionen: sin(α) = cos(β) = a/c. cos(α) = sin(β) = b/c. tan(α) = cot(β) = a/b.Die Winkelfunktionen gelten grundsätzlich nur in rechtwinkligen Dreiecken. die jeweils entsprechenden Seitenlängen der beiden Figuren im gleichen Verhältnis zueinander stehen.
Wann nimmt man Sinus und wann Cosinus : Der Sinus eines Winkels ist das Verhältnis der Länge der Gegenkathete (Kathete, die dem Winkel gegenüberliegt) zur Länge der Hypotenuse (Seite gegenüber dem rechten Winkel). Der Kosinus ist das Verhältnis der Länge der Ankathete (das ist jene Kathete, die einen Schenkel des Winkels bildet) zur Länge der Hypotenuse.
Welche trigonometrische Funktion gibt es wirklich
Trigonometrische Funktionen – Schaubilder
| Funktion | Schaubild |
|---|---|
| Sinus | Abbildung 1: Schaubild der Sinusfunktion |
| Kosinus | Abbildung 2: Schaubild der Kosinusfunktion |
| Tangens | Abbildung 3: Schaubild der Tangensfunktion |
Wie heißen die drei Winkel : Einteilung nach Winkeln
Dreiecke mit drei spitzen Winkeln heißen spitzwinklige Dreiecke. Dreiecke mit einem stumpfen Winkel heißen stumpfwinklige Dreiecke. Dreiecke mit einem rechten Winkel heißen rechtwinklige Dreiecke. Im rechtwinkligen Dreieck bilden die Katheten den rechten Winkel.
Die Winkelfunktionen Sinus, Kosinus und Tangens verwendest du, wenn du die Länge einer Seite oder die Größe eines Winkels in einem rechtwinkligen Dreieck berechnen möchtest.
Die Tangensfunktion ist periodisch, es gilt tanx=tan(x+k⋅π) (k∈Z). Der Funktionsgraph der Tangensfunktion ist punktsymmetrisch zum Ursprung, sie ist also eine sog. ungerade Funktion. Er ist außerdem auch punktsymmetrisch zu allen Nullstellen (weil die Funktion bis nach „±∞“ periodisch ist).
Für welche Winkel gilt sin cos
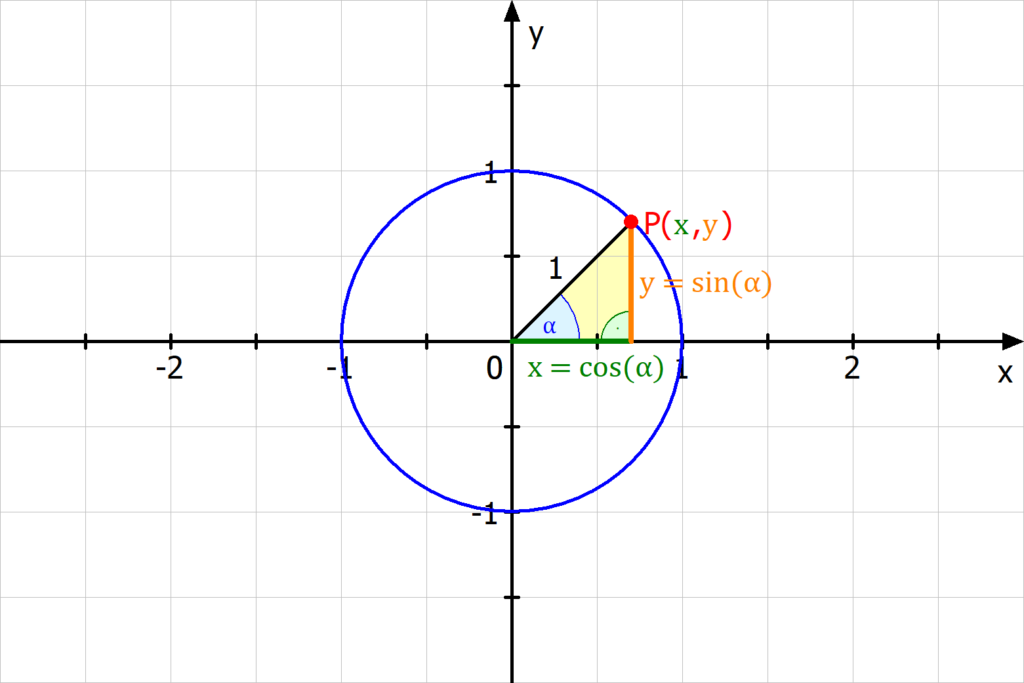
Spiegelst du den Punkt P(x|y) an der x-Achse, dann erhälst du den Punkt P' mit den Koordinaten (x|-y). Liegt der zum Punkt P gehörige Winkel α zwischen 0° und 360°, dann ist der zum Punkt P' gehörige Winkel 360° – α. Wegen x=cos(α) und y=sin(α) gilt dann: cos(360°-α)=x und sin(360°-α)=-y.Definition des Kosinus
Mit dem Kosinus kannst du rechnen, wenn du zwei der drei Größen, Winkel, Ankathete und Hypotenuse gegeben hast und die dritte suchst. Das Vorgehen ist also ähnlich wie beim Sinus, nur mit der Ankathete anstatt der Gegenkathete eines Winkels.Welche Winkelarten gibt es
- Nullwinkel: 0°
- Spitzer Winkel: 0° – 90°
- Rechter Winkel: 90°
- Stumpfer Winkel: 90° – 180°
- Gestreckter Winkel: 180°
- Überstumpfer Winkel: 180° – 360°
- Vollwinkel: 360°
rechte Winkel (α = 90°) stumpfe Winkel (90° < α < 180°) gestreckte Winkel (α = 180°) überstumpfe Winkel (180° < α < 360°)
Wo finde ich Winkel im Alltag : Im Alltag begegnen uns Winkel überall: Dächer haben einen Neigungswinkel, jede Tür steht mit einem bestimmten Winkel offen, Flugzeuge heben von der Startbahn mit einem bestimmten Winkel ab, Straßen haben Steigungswinkel, geometrische Figuren haben Winkel und es gibt noch viele weitere Beispiele.
Was ist Arctan Formel : Die Funktion ARCTAN (= Arcustangens) ist die Umkehrfunktion der Funktion TAN: Sie liefert den inversen Tangens einer Zahl – also den Winkel, dessen Tangens Zahl ist. Das Ergebnis wird im Bogenmaß (Radiant) geliefert. Tipp: Mit der Funktion GRAD können Sie das Ergebnis vom Bogenmaß in Grad umrechnen.
Was ist der Tangens von 30 Grad
sin cos tan Tabelle
| Winkel α im Gradmaß | tan(α) gerundet |
|---|---|
| 0° (360°) | 0,0000 |
| 15° (-345°) | 0,2679 |
| 30° (-330°) | 0,5774 |
| 45° (-315°) | 1,0000 |
Spiegelst du den Punkt P(x|y) an der x-Achse, dann erhälst du den Punkt P' mit den Koordinaten (x|-y). Liegt der zum Punkt P gehörige Winkel α zwischen 0° und 360°, dann ist der zum Punkt P' gehörige Winkel 360° – α. Wegen x=cos(α) und y=sin(α) gilt dann: cos(360°-α)=x und sin(360°-α)=-y.Allgemein kann man sagen, dass Winkel bis 10° als kleine Winkel angesehen werden dürfen. Betrachtet man die verschiedenen Winkelfunktionen am Einheitskreis, wird die Herleitung dieser Näherungen klar.
Wann benutzt Ich Sinus : Sinussatz. Den Sinussatz kannst du benutzen, um fehlende Stücke eines Dreiecks zu berechnen. Zum Beispiel, wenn zwei Seitenlängen und ein gegenüber liegender Winkel oder eine Seitenlänge und zwei Winkel gegeben sind. Das Dreieck muss dabei nicht rechtwinklig sein!